TL;DR

Unlocking Physiological Insights from Consumer Wearables

This research investigated whether consumer wearables can reliably capture complex physiological variations across the menstrual cycle. Through two complementary studies, I demonstrated that continuous sensing from smartwatches and glucose monitors can reveal meaningful hormonal and metabolic patterns, opening new possibilities for accessible health monitoring.

Two-Phase Research Program

Temperature-Hormone Relationships

Investigating correlations between wrist-worn temperature sensors and daily hormone fluctuations across menstrual cycles

Glucose-Cycle Dynamics

Examining blood glucose variations and their relationship to menstrual phases using continuous glucose monitoring

Total Participants

~180~

Menstrual Cycles Analyzed

3500+

Days of Wearable Data

~50

Tracked Signals Per Participant

The Problem

Limited accessibility of hormonal and metabolic health monitoring

Understanding physiological variations across the menstrual cycle typically requires expensive clinical testing and infrequent sampling. Consumer wearables generate continuous data streams, but their potential for capturing meaningful hormonal and metabolic patterns remains largely unexplored in in-the-wild longitudinal studies.

Clinical testing is inaccessible and sparse

Traditional hormone testing requires clinical visits, is expensive, and provides only snapshot measurements rather than continuous tracking of physiological changes throughout menstrual cycles.

Untapped potential of consumer devices

Modern wearables continuously collect temperature, glucose, and activity data, but we lack systematic understanding of how these signals relate to underlying hormonal and metabolic processes across reproductive health cycles.

What I Did

📊

Statistical Modeling

Designed and implemented hierarchical linear mixed-effects models to analyze hormone-temperature and glucose-cycle relationships

🔬

Longitudinal Study Design

Coordinated 3-month data collection protocol with multimodal sensing across 49 participants

📈

Signal Processing

Developed preprocessing pipelines for continuous physiological data including filtering, interpolation, and peak detection

Research Approach

Research Goal

Can consumer wearables provide clinically meaningful insights into hormonal and metabolic variations across the menstrual cycle through continuous, accessible monitoring?

How do wrist-worn temperature measurements correlate with daily hormone fluctuations?
What are the temporal relationships between hormone peaks and physiological signal changes?
How does blood glucose vary systematically across menstrual cycle phases?
What confounding factors must be controlled for in consumer device studies?

Phase 1: Temperature-Hormone Study

Devices: Dexcom G6 CGM,, Fitbit Sense (WST), Mira Plus (LH, E3G hormones)

Duration: 3 months continuous collection per participant

Analysis: Linear mixed-effects models with random slopes/intercepts, quadratic terms, hormone interactions

Outcome: 45 participants, 123 analyzable cycles

Phase 2: Glucose-Cycle Study

Devices: Dexcom G6 CGM, Fitbit Sense, Mira Plus

Duration: 3 months with daily self-report diaries

Analysis: Univariate and multivariate models controlling for step count, food cravings, fatigue, sleep

Outcome: 49 participants, 149 analyzable cycles

98.3%

Fitbit Data Completeness

86.8%

CGM Data Completeness

90.3%

Self-Report Completeness

⚠️ Technical Decision

Used validated consumer devices (Fitbit Sense, Dexcom G6, Mira Plus) rather than clinical-grade equipment to evaluate real-world accessibility. All devices, in prior literature, showed strong correlations with clinical methods: Fitbit PBT ±0.23°C vs. clinical thermometry, Dexcom 98.7% accuracy vs. lab glucose, Mira 99% ovulation prediction accuracy.

Technical Analysis Framework

Data Preprocessing & Signal Processing

Applied systematic preprocessing with different approaches for temperature vs. glucose data. Temperature signals required noise reduction due to sensor variability, while glucose data needed cycle-aware temporal modeling to capture periodic patterns.

 Temperature Signal Processing (Phase 1): 5th-order Butterworth low-pass filter with 10% cutoff frequency
Linear interpolation for temporal standardization (1 sample/day)
Peak detection via "three-over-six rule" (≥0.2°C elevation for ≥3 days)
Hormone peak identification: Local maxima >1.3× E3G, >2.2× LH baseline ratios
 

 Glucose Signal Processing (Phase 2): Daily median calculation from 5-minute CGM readings (288 samples/day)
LOESS smoothing for trend visualization across normalized cycles
Restricted cubic spline analysis for periodic pattern detection
Quality control: ≥18 hours continuous data per day requirement
 

LOESS Smoothing & Temporal Visualization

Implemented LOESS (Locally Estimated Scatterplot Smoothing) regression to visualize physiological trends across normalized menstrual cycles. This non-parametric approach revealed biphasic patterns without assuming specific functional forms.

LOESS-smoothed trends revealing biphasic patterns in temperature (Phase 1) and glucose (Phase 2) across normalized menstrual cycles

LOESS smoothed trends showing temperature patterns across menstrual cycles

LOESS smoothed trends showing glucose patterns across menstrual cycles

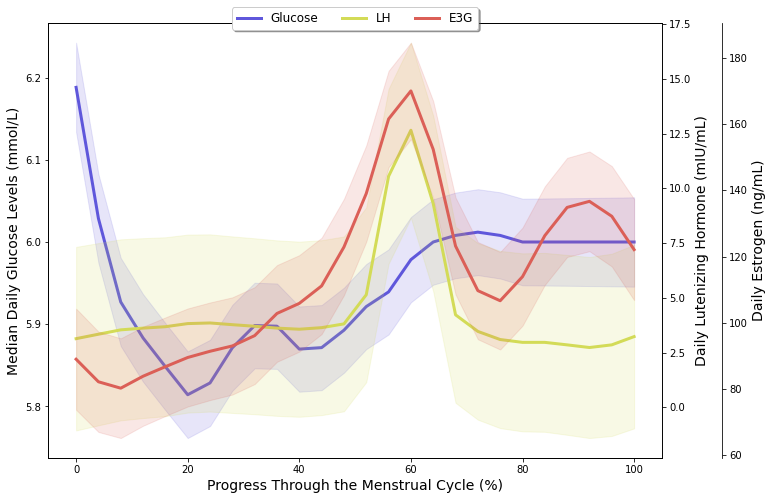
Periodic Spline Analysis & Cycle Modeling

To analyze daily glucose variation across the menstrual cycle, a generalized linear model (GLM) was fitted using restricted cubic splines (RCS). Knots were empirically determined from the data using rcspline.eval(), providing five internal knots that flexibly capture non-linear trends in glucose levels across the normalized cycle timeline.

Model Specification:

median_glucose ~ rcs(cycle_percent_shift, knots = c(...))

Custom plotting was applied using the plot_model() function to visualize the spline-predicted relationship between cycle progression (%) and median daily glucose levels (mmol/L). Plot aesthetics were standardized using set_theme() to ensure consistency across figures, with enhanced label visibility and axis clarity.

Visualization:

plot_model(model_cs_per, type = "pred", axis.title = c("Progress Through the Menstrual Cycle (%)", "Daily Median Glucose Levels (mmol/L)"))

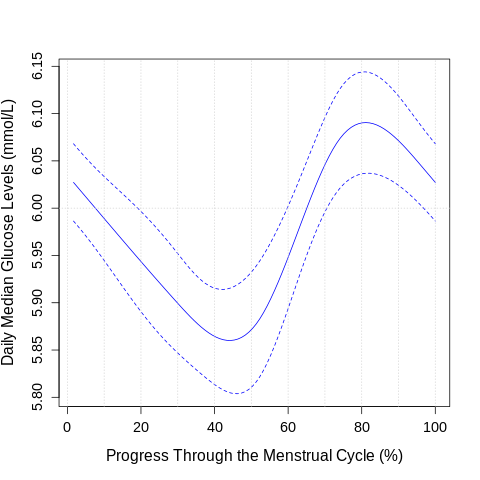
Restricted cubic spline fit showing glucose variation across normalized cycle progression

Hierarchical Mixed-Effects Modeling

Implemented phase-specific linear mixed-effects models with different structures for temperature vs. glucose analyses. Temperature models focused on hormone-physiology relationships, while glucose models emphasized phase-based comparisons. All results of models were reported according to β-coefficients, 95% CI, and the significance of each relationship within models, considering a statistical significance threshold of p<0.05. I applied Holm-Bonferroni adjustments to correct for multiple comparisons.

Example Temperature Model Structure (Phase 1):

WST ~ E3G + LH + E3G² + LH² + E3G×LH + confounds + (1+cycle|participant_id)

Hormone predictors centered by individual participant means
Quadratic terms to capture non-linear relationships
Interaction terms between estrogen and luteinizing hormone
Random slopes for cycle effects within participants

Example Glucose Model Structure (Phase 2):

glucose ~ phase + E3G + confounds + (1|participant_id)

Phase as categorical predictor (late-follicular reference)
Linear hormone effects (E3G as continuous predictor)
Systematic confound testing and multivariate adjustment
Random intercepts only (no cycle-level random effects)

Confound Control & Multivariate Analysis

Systematically tested potential confounders including demographics, physical activity, stress, sleep quality, and food cravings. Built multivariate models to isolate hormone-physiology relationships from lifestyle factors. Also built models stratified by phases.

Confounding Variables Tested:

Physiological

Daily step count
Sleep duration/quality
Heart rate variability

Behavioral

Self-reported physical activity
Food cravings (6-point scale)
Stress levels

Demographic

Age, BMI, height, weight
Cycle length variability
Previous contraceptive use

Temporal Alignment Analysis

Built peak detection algorithms to identify hormone surges and corresponding physiological responses. Calculated temporal offsets between hormone peaks and temperature changes.

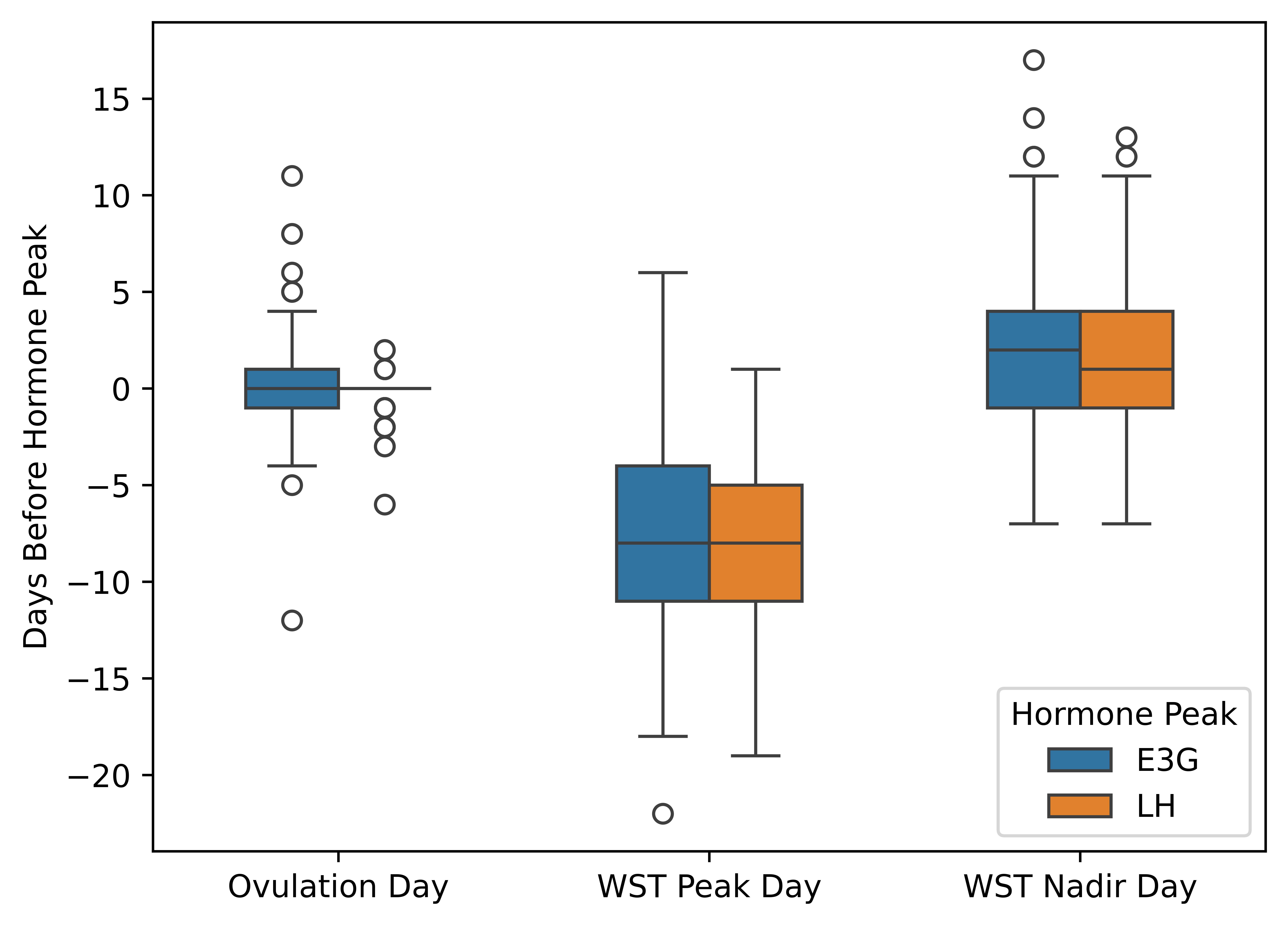
Temporal alignment between hormone peaks and physiological signals

Key Findings

Consumer wearables capture clinically meaningful hormone-temperature relationships

Wrist-worn temperature sensors successfully detected biphasic patterns correlating with hormonal fluctuations:

Linear LH-temperature relationship: β = -0.002°C per mIU/mL (p < 0.001, CI: [-0.004, -0.0009])
Phase-specific E3G effects: Higher estrogen → lower WST during ovulation (quadratic term significant)
Temporal alignment: WST nadirs occurred 2.3±4.5 days before E3G peaks, WST peaks 8.2±4.2 days after
Robust to confounds: Relationships persisted after controlling for glucose, activity, stress, and sleep quality

Glucose exhibits systematic biphasic variation across menstrual cycles

Continuous glucose monitoring revealed consistent metabolic patterns synchronized with reproductive cycles:

Phase-specific elevation: Luteal phase glucose 0.16 mmol/L higher than late-follicular (p < 0.001)
Ovulation increase: Significant 0.08 mmol/L elevation during fertile window (p < 0.05)
Estrogen correlation: Higher E3G levels → lower glucose (β = -0.0003, p < 0.01)
Behavioral interactions: Food cravings amplified glucose elevation during luteal phase

Individual variability requires personalized modeling approaches

Hierarchical modeling revealed substantial between-person differences requiring individualized baselines:

Timing variability: Hormone-temperature alignments varied ±4.5 days between individuals
Cycle length effects: Relationships scaled with individual cycle duration (28.0±8.7 days)
Random effects significance: Individual intercepts and slopes essential for model validity

Quantitative Results

Analysis	Significant Relationships	Statistical Significance
Phase 1: WST-Hormone Models	Linear LH → WST (full cycle) Quadratic LH → WST (full cycle, luteal) Quadratic E3G → WST (ovulation) E3G × LH interaction (full cycle)	p < 0.001 p < 0.01 p < 0.05 p < 0.001
Phase 2: Glucose-Cycle Models	Ovulation phase elevation Luteal phase elevation Estrogen correlation Step count (protective)	p < 0.05 p < 0.001 p < 0.01 p < 0.001
Confound Control	Sleep issues → higher WST High activity → lower WST Food cravings → higher glucose Demographics: non-significant	p < 0.05 p < 0.05 p < 0.001 p > 0.05

💡

Research Impact

This work demonstrates that consumer wearables can capture clinically meaningful physiological variations. The hierarchical modeling approach and longitudinal design provide a template for evaluating other consumer health technologies in reproductive health contexts.

Technical contribution: Longitudinal analysis of consumer wearable accuracy for hormone and metabolic tracking

Clinical impact: Evidence base for accessible reproductive and metabolic health monitoring

Methodological framework: Statistical approaches for consumer device validation in health applications

Consumer devices are increasingly used to monitor peripheral body temperature (PBT) for menstrual cycle tracking, but the link between PBT and hormone variations remains underexplored. This study examines the relationship between these variables with a focus on nightly wrist skin temperature (WST). Fifty participants provided physiological and self-reported data, including WST, daily step counts, glucose levels, hormone levels (E3G, LH), and diary entries. Results show a negative correlation between WST and hormone levels when E3G and LH are below average, and this trend was robust to demographics and self-reported stress. Increased variance between mid-cycle hormonal peaks and WST fluctuations may stem from differences between basal body temperature (BBT) and WST. This research suggests that algorithms reliant on body temperature for tracking hormonal changes or other aspects of the menstrual cycle may need to account for increased variance in WST trends if they are meant to be deployed on wearable devices.

Past studies on how blood glucose levels vary across the menstrual cycle have largely shown inconsistent results based on limited blood draws. In this study, 49 individuals wore a Dexcom G6 continuous glucose monitor and a Fitbit Sense smartwatch while measuring their menstrual hormones and self-reporting characteristics of their menstrual cycles daily. The average duration of participation was 79.3±21.2 days, leading to a total of 149 cycles and 554 phases in our dataset. We use periodic restricted cubic splines to evaluate the relationship between blood glucose and the menstrual cycle, after which we assess phase-based changes in daily median glucose level and associated physiological parameters using mixed-effects models. Results indicate that daily median glucose levels increase and decrease in a biphasic pattern, with maximum levels occurring during the luteal phase and minimum levels occurring during the late-follicular phase. These trends are robust to adjustments for participant characteristics (e.g., age, BMI, weight) and self-reported menstrual experiences (e.g., food cravings, bloating, fatigue). We identify negative associations between each of daily estrogen level, step count, and low degrees of fatigue with higher median glucose levels. Conversely, we find positive associations between higher food cravings and higher median glucose levels. This study suggests that blood glucose could be an important parameter for understanding menstrual health, prompting further investigation into how the menstrual cycle influences glucose fluctuation.

Modeling Wearable and Physiological Data Relationships